) 五:板书设计: 一元一次方程的应用:例题:小黑板出示例1 题目解:设原来有x 千克面粉,那么运 相等关系:原来重量—运出重量=剩余重量出了15%x 千克,依题意,得 等式左边:等式右边:x—15%x= 原来重量为x 千克,剩余重量为 千克。一般 解一元一次方程式 分數型判斷相同的解 Youtube 一般 解一元一次方程式 分數型除錯 Youtube 高校数学 3元連立1次方程式 一般型と循環型 受験の月 完整的题型 完美的解法 全解一元一次方程 初中数学 学习资料大全 免费学习资源下载 子供向けぬりえ 1一元一次方程: 只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程。 2一元一次方程的标准形式: axb=0(x是未知数,a、b是已知数,且a≠0)。 3条件:一元一次方程必须同时满足4个条件: (1)它是等式;

一元一次方程计算题汇总下载 Word模板 爱问共享资料
一元一次方程式题目国中
一元一次方程式题目国中- 一元二次方程公式法题 —— 记住用公式法解一元二次方程的步骤 例如 3x7x= 2 第一步先把方程变成 ax bx c=0这样的一般形式3x7x 2=0 (右边一定要是0) 第二步写出各项的系数 a=3,b=7,c=2 第三步计算出b4ac这个特殊式子(叫判别式)的值b4ac=( 初三一元二次方程公式法题目急求解(3 y)平方=2y(y 3)3x平方 (x2)平方2x=0手机不太方便打符号将就着看吧过程 一元一次方程解应用题典型例题1、分配问题: 例题1、把一些图书分给某班学生阅读,如果每人分3 本,则剩余 本;如果每人分4 本,则还缺25 本问这 班有多少学生?
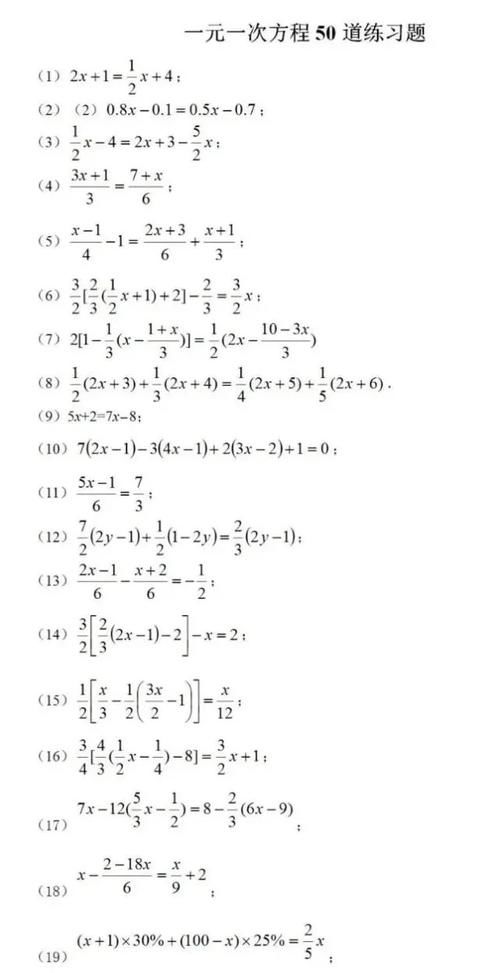



一元一次方程题目和答案
一、内容和内容解析 1 .内容 二次函数与一元二次方程. 2 .内容解析 " 一元二次方程和二次函数是 " 是 " 数与代数 " 领域中重要的内容,其内容的复杂性、综合性和思想性都很强,在第三学段占有重要地位.本 节,是在学生学习了二次函数的概念、图象、性质的基础上,让学生继续探索二 初接触一元一次方程,该怎么学 一元一次方程思维结构图 在生活中,我们会遇到各式各样的问题,仔细想想,数学与现实生活联系十分紧密。 同时在我们的学习过程中,一元一次方程是一元二次方程的基础。 今天我们就先讲几个小例子,同学们思考一下跟我们的现实生活有什么联系呢?一元二次方程知识点解析和题型汇总 老刘说数学 老师 25 人 赞同了该文章 E=MC2是爱因斯坦留给人类的伟大贡献,也是人类历史上最伟大的十大公式之一,她揭示了物质的两个属性,物质的质量和能量之间的本质关系,是近代物理的理论基础,而我们即将学习
一元二次方程经典题型汇总pdf,一元二次方程经典题型汇总 一、一元二次方程的概念 1、一元二次方程:含有一个未知数,并且未知数的最高次数是 2 的整式方程叫做一元二次方程。 2、一元二次方程的一般形式: ax 2 bx c 0(a 0) ,它的特征是:等式左边十一个关于未知数 x 的二次多项式,等式右边是《一元一次方程》易错题汇总 一、解方程和方程的解的易错题: 一元一次方程的解法: 重点:等式的性质,同类项的概念及正确合并同类项,各种情形的一元一次方程的解法; 难点:准确运用等式的性质进行方程同解变形(即进行移项,去分母,去括号,系数化一等 步骤的符号问题,遗漏问题); 学习要点评述:对初学的同学来讲,解一元一次方程的方法很容易掌握,但 第二十一章 一元二次方程 第1课时 一元二次方程的概念 学 习 目 标 1了解一元二次方程的概念 2掌握一元二次方程的一般形式、相关项及系数等概念 3应用一元二次方程的概念解决一些简单题目 知识要点 1等式两边都是整式,只含有一个未知数(一元),并且
把 一 元 二 次 方 程 化 为 一 般 形 式 是 ________________ , 其 中 二 次 项 为 : ______,一次项系数为:______,常数项为:______ 2写出一个有一根为 的一元二次方程___________________ x 3已知三角形两边长分别是 2 和 9,第三边的长为一元二次方程 2 14x48=0 的一个 根,则这个三角形的周长为 。 4关于 x 一元二次方程 2x (kx4)x26=0 没有实数根,则 k 的最小整数值是______。 我们都知道一元二次方程是很容易解的,但一元三次方程就不同了。 所以我们故事的起因就是一位意大利数学家费罗。 他在长期的钻研中找到了无二次项一元三次方程的解法的公式。 意大利数学家费罗 找到公式后,费罗担心这个成果发表出来后可能会引起震惊,所以到死都没有把这个成果发表。 他死前把自己的研究成果传给了自己的女婿 纳夫 和弟子 菲尔 。 后来 消元——解二元一次方程组 课时设计 课堂实录 消元——解二元一次方程组 1第一学时 教学活动 活动1导入1、创设情境引入新知: 利用多媒体教学手段,创设情境,通过村子里老人们故意刁难读书的学生的问题引入教学,情境活泼、自然。



Search Q E4 B8 80 E5 85 E4 B8 80 E6 Ac A1 E6 96 B9 E7 A8 8b E7 E4 B9 A0 E9 98 E5 B0 8f E5 Ad A6 Tbm Isch




19年初一寒假数学提升练习题 解一元一次方程 北京爱智康
北京西点培训 > 二元一次方程配方顶点式题目 > 列表 (17,18)—一次函数解析式的确定与应用,二元一次方程组(代入消元法)2、配方法 将一元二次方程配方成(xm)^2=n的形式再求解 03 3、求根公式法 把方程化为一般式ax^2bxc=0 求出判别式 =b^24ac≥0的情况下使用求根公式求解3元一次方程题目和答案 来源:wwwzuowenzhaicom 投稿: 50道三元一次方程组计算题及答案过程 : 12x7yz=24 ① 4x4yz=3 ② xy=5 ③ 解由①②得2x7yz4x4yz=243 6x3y=21 ④ 得6x3y=21 ④ xy=5 ③ 解由③得x=5y ⑤ 把⑤代入④中 306y3y=21 3y=9 y=3 因此x=2 y=3 z=1 2




國一數學一元一次方程式 第一題不知道為什麼答案是那個樣子 第二題是不知道哪裡算錯 Clear
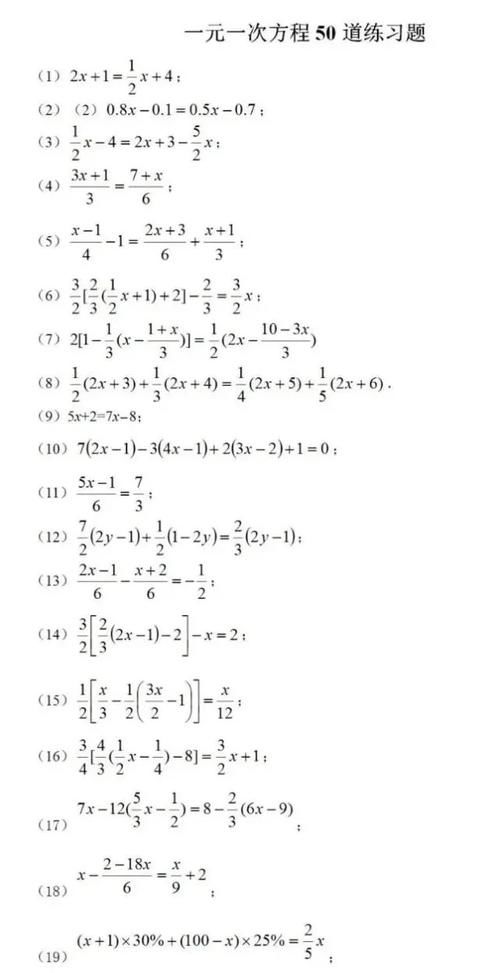



一元一次方程题目和答案
今天,由小锐老师给大家带来三元一次方程组的解题思路。 题型1 (一)思路: 做三元一次方程,大家都觉得很麻烦,各种x, y, z,不停地计算,但是我希望这种抱怨只停留在"麻烦"这个层面,千万不要误认为,三元一次方程组是"难题"! 早在我们学二元一次方程组的时候,我就和大家讲述过,"为什么我们不会做二元一次方程组",其实只不过是因为多了一个 一、教学目标 1、知识与技能目标:认识一元二次方程,并能分析简单问题中的数量关系列出一元二次方程。 2、过程与方法:学生通过观察与模仿, 建立起对一元二次方程的感性认识,获得对代数式的初步经验,锻炼抽象思维能力。1.一元二次方程的定义 一元二次方程有三个特点:(1)只含有一个未知数;(2)未知数的最高次数是2;(3)是整式方程.要判断一个方程是否为一元二次方程,先看它是否为整式方程,若是,再对它进行整理.如果能整理为 (a≠0)的形式,则这个方程就为一元二次方程. 2.一元二次方程的一般形式 我们




一元一次方程 搜索结果 哔哩哔哩 Bilibili



备战期中 一元一次方程应用题型分析及练习 期中考前必做
一元一次方程应用题(怎样才能学好) 首先未知数一定要明确,往后就不难了。 依照条件,和自己设的未知数列出方程,有的题目需要运用好几次未知数,那就是一个经验问题了。 加油吧! 相信你一定能学好! ! 这些方法只不过起一个过渡作用,真正学好方程并不需要。 加一点:你在看题目时先看问题,然后仔细地看有什么条件,看看哪些是已知的,哪些是未知 211 一元二次方程 初中数学 人教11课标版 1教学目标 ~1、知识技能 探索一元二次方程及其相关概念,能够辨别各项系数;能够从实际问题中抽象出方程知识。 2、数学思考 在探索问题的过程中使学生感受方程是刻画现实世界的一个模型,体会方程与实际生活数学教案-用公式法解一元二次方程 第1教时教学内容: 121 用公式解一元二次方程(一)教学目标:知识与技能目标:1.使学生了解一元二次方程及整式方程的意义;2.掌握一元二次方程的一般形式,正确识别二次项系数、一次项系数及常数项.过程与方法目标: 1.通过一元二次




十道一元一次方程的题求10道以上一元一次方程的应用题




解一元一次方程50道练习题带答案资料 豆知网
1分数形式的一元一次方程的解题步骤: (1)去分母(根据等式的性质2,方程两边乘以各分母的最小公倍数) (2) 去括号(根据分配律) (3) 移项 (根据等式性质1) (4)合并,把方程化为ax=b (b=0)的形式 (逆用分配律) (5) 化系数为1,得到方程的解x= b/a (根据等式性质2) 2举例说明:(我课件中的截图) 本回答被网友采纳 87布置教材P27第一题本节课我们要掌握哪些东西? 1.必做:教材P27习题2 2.选做:若x22xm13=0是关于x的一元二次方程,求m的值 回忆一元一次方程 试着计算该题 理解"一元二次方程"的概念 根据题意列方程 (1)都只含一个未知数x;(2)它们的最高次数都是2次的; (3) 都有等号,是方程. 找出二次项、二次项系数、一次项、一次项次数和常数项解:3x(x1)=5 (x2)可试题提示:只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形 式是axb=0(a,b是常数且a≠0),高于一次的项系数是0. 解:由一元一次方程的特点得m﹣2=1,即m=3, 则这个方程是3x=0, 解得:x=0. 故选A.



初一上册数学第三章 一元一次方程 练习题 初一数学 中考网



七年级数学一元一次方程50道练习题 含答案 侵权
只含有一个未知数(一元),并且未知数项的最高次数是2(二次)的整式方程叫做一元二次方程 1 。一元二次方程经过整理都可化成一般形式ax²bxc=0(a≠0)。其中ax²叫作二次项,a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项 2 。 解一元二次方程步骤: ①求b4ac的值,大于0有解,小于0无解 ②有公因式先提公因式 ③公式法(完全平方公式,平方差公式)一元二次方程的根与系数的关系 以两个数x1,x2为根的一元二次方程(二次项系数为1)是x^2(x1x2)xx1?x2=0 相 21年中考数学一元二次方程:判别式 中考网整理了关于21年中考数学一元二次方程:判别式,希望对同学们有所帮助,仅供参考。



一元一次方程100道 万图壁纸网




50道一元一次方程带解题步骤 百度经验
解一元一次方程的一般步骤:(1) 去分母:方程两边同时乘以各项分母的最小公倍数;例题6:为下面方程去分母:;(2) 去括号:可先去小括号,再去中括号,最后去大括号(也可以按照自己擅长的方式去括号);例题7:去括号:2 (x3)-5 (1-x)=3 (x-1)(3一元一次方程指只含有一个未知数、未知数的最高次数为1且两边都为整式的等式。 一元一次方程只有一个根。 一元一次方程可以解决绝大多数的工程问题、行程问题、分配问题、盈亏问题、积分表问题、电话计费问题、数字问题。 1 一元一次方程最早见于约公元前1600年的古埃及时期1 。 公元0年左右,数学家花拉子米在《对消与还原》一书中提出了"合并同类项 一元一次方程,同学们将会在初一接触到它,实际,解一元一次方程还是很简单的,下面小编就为你解一道一元一次方程,相信聪明的你看完小编的例题后就能够举一反三啦! 工具/原料 more 本子 笔 方法/步骤 1 /6 分步阅读 第一,列出方程。当我们解一道方程




初中一元一次方程5大解题技巧 8大例题 赶紧掌握 教育频道 手机搜狐




七年级上册一元一次方程练习题带答案 初中电子课本




數學一點也不無聊 教學活動 兩步驟一元一次方程式閃卡 搭配單元 一上一元一次方程式




一元一次方程式的解题方法与技巧 自学习网




一元一次方程计算题汇总下载 Word模板 爱问共享资料




解一元一次方程计算题每天训练 15分钟 每日头条




初一数学一元一次方程概念与解题方法例题解析 三好网



方程式计算题 万图壁纸网



人教版七年级数学上册一元一次方程解应用题专题练习 松鼠文库



第六道题 一元一次方程解 信息评鉴中心 酷米资讯 Kumizx Com



1



最新人教版七年级上册数学一元一次方程应用题 及答案 Doc 教育文库 教育资源网 新时代文库www Xsdwk Com 教育文库 教育资源网 新时代文库www Xsdwk Com



基础题一样很重要 初中数学解方程100练 一元一次一元二沪教版与苏教版初中数学哪个难次 小初高题库试卷课件教案网




小学一元一次方程练习题 整数 Pdf 万象文库www 2wx Com



方程题100道带答案 万图壁纸网



解一元一次不等式专项练习87题 有答案 松鼠文库



四年级奥数题 简单一元一次方程例题及巩固练习 四年级奥数题 奥数网




一元一次方程应用题题型 初中电子课本网




小学五年级方程练习题下载以及教学 宝宝学习网




一元一次方程应用题典型例题答案 豆知网



解一元一次方程的练习题 松鼠文库



中考数学指导 一元一次方程练习题及答案 一元一次方程资讯 新东方在线移动版




一元一次方程实际问题解题方法 百度经验



100道一元一次方程计算题 绿色文库网




简单的一元一次方程练习题下载 Word模板 爱问共享资料



一元一次方程的计算和练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则




國中數學總複習 5 一元一次方程式 莫博士 帶你長知識 大師鏈 全球華人價值內容平台




关于x的一元一次方程ax B的解法 网上竟然有那么多的争论 知乎



一元一次方程6 1 6 2水平测试 1 华七下第六章 6 2解一元一次方程 初中华师大版 数学中国网



一元一次方程练习题及答案 松鼠文库




列一元一次方程解应用题专项练习 Doc 文档分享网



北师大版七年级数学上册第五章 一元一次方程 练习题及答案 莲山课件



必备初一上册数学课后练习题 一元一次方程 数学同步练习 精品学习网



悟空问答 初一学生数学只考了1分 一元一次方程听不懂该怎么办 46个回答



七年级数学一元一次方程50道练习题 含答案 侵权



一元一次方程计算题难 解一元一次方程道经典练习题 包含各种复杂方程 简明教程



解一元一次方程50道练习题 经典 强化 带答案 松鼠文库




60道一元一次方程带答案 搜狗搜索



七年级数学一元一次方程打折销售经典练习题及答案



一元一次方程练习题 道 分享答案一元一次方程练习题分享30道 励志名言网



初一数学一元一次方程 搜狗图片搜索



初一数学丨第3章一元一次方程高频考点汇总 单元检测试卷附答案 新闻 蛋蛋赞




解一元一次方程50道练习题 带答案 Doc 在线文库www Lddoc Cn 在线文库www Lddoc Cn




解一元一次方程100题 七年级数学 吾爱数学首页 初中数学学科资源 初中数学备课资源下载




七上数学第三章 一元一次方程 知识点 名师精选练习题 可打印 济南招商加盟 济南论坛网 手机版 Powered By Discuz




初中一元一次方程易错题及其解析



中考数学指导 一元一次方程练习题及答案 一元一次方程资讯 新东方在线移动版




简单的一元一次方程练习题下载 Word模板 爱问共享资料



七年级数学a卷题 第6章一元一次方程 衡课网 衡课网



一元一次方程练习题 预初年级 上海奥数网



完整的题型 完美的解法 全解一元一次方程 初中数学 学习资料大全 免费学习资源下载




七年级数学上册 一元一次方程应用题专项练习 期末巩固提升必备 网易订阅



七年级数学一元一次方程应用题专题练习 初一数学 中考网




简单的一元一次方程练习题下载 Word模板 爱问共享资料



七年级数学一元一次方程50道练习题 含答案 侵权




初中一元一次方程5大解题技巧 8大例题 赶紧掌握 教育频道 手机搜狐



1




75 数学一次方程式 最高のぬりえ




50 グレア一元一次方程式题目




國中數學認識一元一次方程式 Youtube



名師課輔網 一元一次方程式技巧



人教版 初一数学一元一次方程练习题 数学练习题 成都中考网



青岛版数学七年级上册第7章 一元一次方程 检测题 Word版含答案 启达教育网中小学辅导网 一对一 小班课 托管班 课外辅导补习班 启达教育官网



1




初中数学 一元一次方程常考的13种应用题 掌握考高分 知乎



初一高中解一元一次方程 合并同类项与移项 练习题30道13南充技能素质数学年 高中课题目



版一元一次方程的解法练习题 Docx 教育文库 教育资源网 新时代文库www Xsdwk Com 教育文库 教育资源网 新时代文库www Xsdwk Com




请提供一些一元一次方程去分母练习题 快资讯




一元一次方程例题解析求40道一元一次方程计算题



17年小升初衔接数学一元一次方程应用题 小升初衔接 奥数网




解一元一次方程计算题每天训练 15分钟 自学习网



一元一次不等式练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则




解一元一次方程50道练习题经典 强化 带答案 豆知网



解一元一次方程习题精选附答案 松鼠文库




解方程练习题推荐品牌 新人首单立减十元 21年6月 淘宝海外




一元一次方程计算题 Doc 在线文库www Lddoc Cn 在线文库www Lddoc Cn




一元一次方程式應用題 1 1 2 Youtube




列一元一次方程解应用题专项练习180题有答案 豆知网



初一 一元一次方程 应用题归类分析 你可以试试




一元一次方程的解法练习题 爱问共享资料




初一数学一元一次方程测验 Doc 文档分享网



悟空问答 初一学生数学只考了1分 一元一次方程听不懂该怎么办 46个回答



初一 一元一次方程 应用题归类分析 你可以试试




國中數學總複習 5 一元一次方程式 莫博士 帶你長知識 大師鏈 全球華人價值內容平台



人教版七年级数学解一元一次方程练习题 松鼠文库




解一元一次方程50道练习题 3326学习网



中考数学试题考点8 一元一次方程 常见题型一定要掌握 中考 学习资料大全 免费学习资源下载



初一应用题 一元一次方程应用题类型总结 习题二及答案15日更新 初中年级 家长帮




方程七上数学 解一元一次方程道经典练习题 包含各种复杂方程 利财股票网




解一元一次方程50道练习题带答案 豆知网




一元一次方程计算题80道直接打印 豆知网




ぜいたく一元一次方程式解题 最高のぬりえ


